Research project
Classical DFT

PhD research of Jacobus Dijkman
Although less famous than the quantum version used for electronic structure calculations, classical density functional theory (cDFT) remains a very appealing approach to describe fluids. However, similar as in quantum DFT, the accuracy of the theory is hampered by the lack of an exact description of the (free) energy functional. Over the years, various approximations have been developed, albeit with mixed success.
Now, with a team of researchers at the Computational Chemistry Group (Van ‘t Hoff Institute for Molecular Sciences) and the AMLab (Informatics Institute), together with the Debye Institute for Nanomaterials Science and the Institute for Theoretical Physics of Utrecht University, we have developed a machine-learned approximation that can significantly improve cDFT calculations of fluids and vapours.
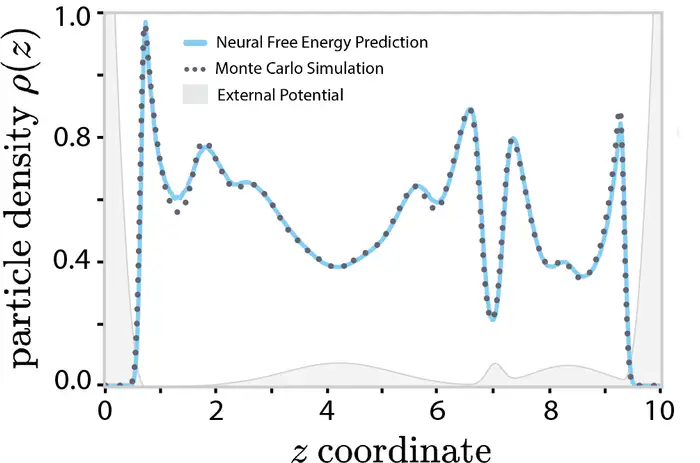
Our ‘neural density functional’ can be trained in two manners. The first approach applies the first functional derivative of the free energy, which requires for training a large dataset of inhomogeneous particle densities on a 3D grid computed with Monte Carlo simulations under various external potentials. This is computationally rather demanding. The second approach, based on the second functional derivatives, requires a dataset of only 1D radial distribution functions of only homogeneous densities. This requires significantly fewer simulations.
Remarkably, we were able to show that the second approach works as well as the first for a simple Lennard-Jones liquid in a 1D planar symmetry. Work is underway to apply the new method to more practical applications.
Joint work with Max Welling, Jan-Willem van de Meent, Bernd Ensing, Marjolein Dijkstra, and René van Roij,
Papers
- Learning Neural Free-Energy Functionals with Pair-Correlation Matching
Jacobus Dijkman, Marjolein Dijkstra, René van Roij, Max Welling, Jan-Willem van de Meent, and Bernd Ensing,
Phys. Rev. Lett. 134, 056103 (2025)
